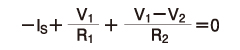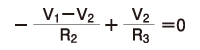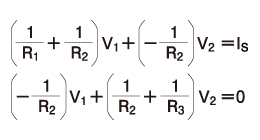番外編 アナログ回路設計のエンジン(後編):Analog ABC(アナログ技術基礎講座)(1/2 ページ)
前回は回路シミュレータを使って、直流解析と交流解析、過渡解析という3種類の解析が実行できることを紹介しました。今回は、解析のメカニズムについて紹介しましょう。
前回は回路シミュレータを使って、直流解析と交流解析、過渡解析という3種類の解析が実行できることを紹介しました。解析のメカニズムについて不思議に思った方も多いのではないでしょうか。
「ネットリストを基に回路の接続状態をどのように理解するのか」、あるいは「周波数や時間の変化に伴って変わるインピーダンスを基に、電圧や電流をどのように計算するのか」など、疑問はいろいろと浮かびます。
長年アナログ回路設計に携わっている著者にも詳細は分かりません。ですが、「NODAL ANALYSIS」と呼ぶ解析がすべての基本になっています。NODALは、NODEが「こぶ」なので直訳すると「こぶのような」となり、接点(ノード)解析と訳せます。
接点を流れる電流に注目
図1の回路を例にノード解析の概略について説明しましょう。まず、回路情報から連立方程式を立てます。その基本となっている規則は、「the sum of currents in and out of a node is zero(ノード(接点)に流れ込む電流と流れ出る電流の総和はゼロ)」というものです(キルヒホッフの第1法則)。
接点では、電流をためておけないので当たり前のことのように感じますが、これが重要な法則なのです。図1のノードV1について考えると、方程式は以下のようになります。
ここでは、ノードに流れ込む電流を負で、流れ出す電流を正の符号で表します。 次に、ノードV2に着目すると次の式が得られます。
これらの式をV1とV2について整理すると、次の式が得られます。
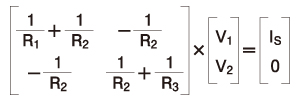
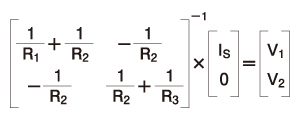
これを行列で表すと、以下の式のようになります。
電圧の値は、逆行列を使った次の計算で求められます。
筆者は行列の計算が苦手なのですが、計算機は得意なようです。逆行列を求める手法はいろいろあります。
この逆行列を使った式で、電流源ISの値を変化させながらノード解析(V1とV2の値の計算)を繰り返したのがDC解析です。抵抗はそのままに、インダクタやコンデンサを、インピーダンスや位相の情報を持つ複素数表記にして計算すれば、AC解析になります。時間の刻み具合に合わせてコンデンサやインダクタを電流源や電圧源で等価的に置き換えて、ノード解析を時間刻みごとに実行しているのが過渡解析です。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- 重量はクジラ級! 超巨大な高NA EUV装置の設置をIntelが公開
- どうする? EVバッテリー リサイクルは難しい、でもリユースにも疑問
- 「GPT-4」を上回る性能で、グラフィカルな文書を読解するLLM技術
- 2023年の世界半導体売上高ランキングトップ20、NVIDIAが初の2位に
- 中国政府の「Intel/AMD禁止令」、中国企業への強い追い風に
- パワー半導体向けウエハー市場、2035年に1兆円台へ
- Intelが高NA EUV装置の組み立てを完了、Intel 14Aからの導入に向けて前進
- Intelの最新AI戦略と製品 「AIが全てのタスクを引き継ぐ時代へ」
- TSMC、24年Q1は増収増益 地震の影響は「最小限にとどまる」
- JDI、次世代有機ELディスプレイ「eLEAP」を24年12月に量産開始へ

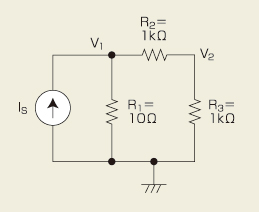 図1 ノード解析が基本 ノード解析では、ノードに流れ込む電流と流れ出す電流が同じであることに注目します。
図1 ノード解析が基本 ノード解析では、ノードに流れ込む電流と流れ出す電流が同じであることに注目します。