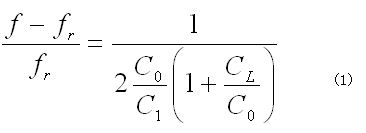第6回 水晶振動子を使うとき知っておくべきこと:水晶デバイス基礎講座(1/2 ページ)
今回は、前回の内容を踏まえ、水晶振動子を使うとき知っておくべきことを幾つか紹介しましょう。
前回(第5回)の内容をまとめると、水晶振動子の発振周波数を調整するには、基本的には主に2つの選択肢があることが分かります。
1つは、水晶振動子の誘導性リアクタンス(ωLe)を調整する方法です。第5回の図2に示した、狭い周波数範囲のどの周波数を発振周波数となるか、水晶振動子の誘導性リアクタンスを調整することで決めることができます。
もう1つは、発振回路側の容量性リアクタンス(1/ωCL)を変える方法です。負荷容量の変化に対する、発振周波数のわずかな差異を、「負荷時共振オフセット」と呼びます。
仮に、発振回路側の要求で、負荷容量(CL)が決まっているとき、水晶振動子の発振周波数の調整は、振動子側のパラメータ(例えば、C0)が担います。一方、水晶振動子側のパラメータが既知の場合、発振周波数を負荷容量(CL)によって、調整することができます。
共振オフセットは振動子の寸法や電極設計で異なる
図1は、負荷容量の変化に対する負荷時共振オフセットの一例です。このオフセット特性は、水晶振動子の寸法や電極の設計などで異なります。ただ、図1から分かるように、負荷容量が小さくなるほど曲線の傾きが急峻(きゅうしゅん)になり、浮遊容量の変化に敏感に影響されます。この結果、発振周波数に誤差が生じたり、発振現象そのものが不安定になったりするので、注意が必要です。
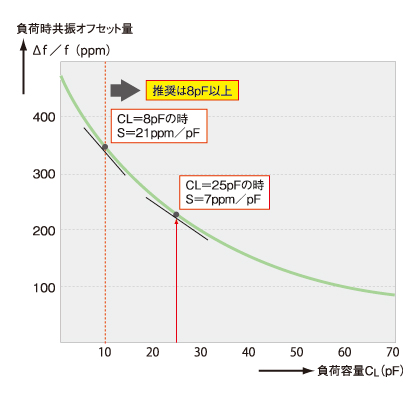 図1 負荷容量の変化に対する負荷時共振オフセットの一例 横軸は負荷容量の値(pF)、縦軸は発振周波数の変化量(負荷時共振オフセット)です。負荷容量が小さくなるほど曲線の傾きが急峻(きゅうしゅん)になり、浮遊容量の変化に敏感に影響されます。図中のCLは負荷容量、Sは曲線の傾きで、負荷容量の変化分に対する共振オフセット量を表します。Sを、「周波数可変感度」と呼びます。
図1 負荷容量の変化に対する負荷時共振オフセットの一例 横軸は負荷容量の値(pF)、縦軸は発振周波数の変化量(負荷時共振オフセット)です。負荷容量が小さくなるほど曲線の傾きが急峻(きゅうしゅん)になり、浮遊容量の変化に敏感に影響されます。図中のCLは負荷容量、Sは曲線の傾きで、負荷容量の変化分に対する共振オフセット量を表します。Sを、「周波数可変感度」と呼びます。負荷容量の変化に対する負荷時共振オフセットは、(1)式のように表現できます。
一般的には、負荷容量を8pF以上に設定することを推奨します。水晶メーカーのカタログには、負荷容量の標準値が記載されていますので、標準値を使用すれば、まず問題はありません。
指定した負荷容量における周波数可変感度(S)は、設計者にとって有用なパラメータです。これは、負荷容量の変化分に対する周波数変化の増加分で定義されています。つまり、図1の曲線を微分した傾きが、周波数可変感度(S)です。周波数可変感度を知ることで、負荷容量を変えたときの発振周波数の変化をあらかじめ知ることができます。
コラム「編集部から筆者への質問」
EE Times EE Times Japan 以前、ATカット型の水晶振動子の発振周波数は、厚みで決まるという説明がありました。一方で、電気的な等価回路の説明では、周波数可変量という指標が出てきます。「発振周波数は、振動子の厚みのみで決まる…」と考えると、等価回路の誘導性リアクタンスによって周波数を変えられることが、うまく整合しないように感じます。
回答:
水晶本来の共振周波数は弾性定数と厚み、形状で決まり、基本的に変わることはありません。本連載では、簡略化のために、ATカット型振動子の発振周波数は、水晶チップの厚みに反比例すると説明しました。ただ、正確には以下のように、水晶チップの弾性係数や密度も考慮する必要があります。
発振周波数(f)=n/2t×(E/p)1/2
n:次数、t:厚み、E:弾性定数、p:密度
例えば、水晶チップに重量を付加するなど機械共振に影響を与えることをすると、電気的な等価回路の定数も変わります。水晶の等価回路がコイルやコンデンサで構成した共振回路のようになるのは、機械共振と機械-電気変換が生じているからです。
水晶に特化せず、物体の固有振動の場合を説明しましょう。物体の固有振動は、その物体の弾性定数と質量に関係します(正確には、形状も関係しますが、簡略化のため、割愛します)。
f=(E/m) 1/2(減衰のない振動のとき)
f:固有振動数、E:弾性定数、m:質量
弾性定数Eが変化しない範囲の外力ならば、固有振動数に影響はありません。しかし、弾性定数が非線型の範囲になってしまうような大きい外力、あるいは集中的な外力を加えると、弾性定数を一定に保てなかったり、質量を変えてしまったりという可能性があります。このような状況では、実際に計測しないと、固有振動数の正確な値を知ることは難しいと思います。
話を水晶に戻し、弾性定数が一定で共振周波数の変化がないとすると、ATカット型水晶振動子の発振周波数は厚みで決定されます。ただし、あくまでも水晶のみの状態でのはなしであり、実際の振動子は水晶の上下に励振用の電極を付ける、つまり質量を付加するため、その電極の質量相当分の水晶の厚みが加算された周波数となります。また、このときの発振周波数は、ネットワークアナライザなどの測定器を使って測定した周波数で表すのが一般的です。
一方、誘導性リアクタンスによる発振周波数の決定は、あくまでも発振回路上でのはなしです。回路側の負荷容量があって初めて成り立ちます。このとき、負荷容量が付いた段階で、回路の発振周波数は若干シフトしますので、この静電容量値を変えることにより、発振周波数を微調整できます。
本文中で紹介したように、水晶の誘導性の領域には、発振回路の発振条件を満足する周波数帯が一定領域あります。負荷容量を付けることにより、発振回路全体のインピーダンスの低い周波数がややずれ、ずれた周波数のほうが安定して発振するようになるのです
以上の話をまとめると、水晶振動子の周波数は電極厚、形状、弾性定数では変わりますが、発振回路に入れることによっては、変わりません。発振回路と組み合わせることで、周波数がずれるのです
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
- ミネベアミツミが日立のパワー半導体事業を買収完了、「ミネベアパワーデバイス」誕生
- NVIDIAのGPU不足は今後も続く ボトルネックはHBMとTSMCの中工程か
- ヤモリの手から着想 接着剤がいらない接着技術を取得、信越化学
- 「カスタムSoC市場2位」、ソシオネクストの成長戦略と先端SoC開発事例
- 村田製作所、23年度は減収減益 電池事業で495億円の減損損失を計上
- ハイエンドスマホのプロセッサはどこまで進化した? 最新モデルで読み解く
- 富士フイルム、ナノインプリントレジストを発売
- ニデックの23年度決算は増収増益も、車載事業は大幅赤字
- 半導体製造の最先端を独走するTSMCの決算から読み取れること
- IntelとAMDのチップ戦略が「逆転」? 最新Core UltraとRyzenを分解