陰湿な人工知能 ~「ハズレ」の中から「マシな奴」を選ぶ:Over the AI ―― AIの向こう側に (8)(5/10 ページ)
数式ゼロのAI解説「ゲーム理論」
ここからは後半になります。この連載の後半は、「私の身の回りの出来事」を使った、「数式ゼロ」のAI解説になります。
さて、本日は、「ゲーム理論」についてお話します。
毎回しつこくて恐縮ですが、「『ゲーム理論』が“人工知能”なのかどうか」については、今回も『江端AIドクトリン』に基づいて私が勝手に判定しました。
まず、「ゲーム理論」についてザックリと説明します。
詳しい話は、こちらをご覧いただくとして、私なりに「ゲーム理論」を定義するとすれば、「最悪の状況下で、最終ラインを確保する戦略理論」です。
分かりにくいと思いますので、もっと簡単に言ってみます。
「合コンで『イケてる男/女』を狙えない立ち位置にあっても、『イケていない男/女』の中から『マシな男/女』を選ぶための戦略理論」です。
「この合コンはハズレだ」と、早々に諦めてしまう人に幸せはやってきません。「ハズレた合コンの中にあって、なお、最良の男/女を求める」人にだけ幸せはやってきます。そう考えれば、ゲーム理論は、幸福の科……もとい、幸福の数理学といえそうです。
そして、この「ゲーム理論」が雄弁に語ることは、戦略なく、ただ「場」に流される人に、幸せはやってこないという事実と、そして、そのような戦略を尽して、なお「最良の選択」が必ずしも「最高の選択」にはならない、という残酷な現実です(ナッシュ均衡(後述))。
ゲーム理論の定番「囚人のジレンマ」
ではまず、ゲーム理論においては、定番中の定番である「囚人のジレンマ」の話から始めます。
「囚人のジレンマ」とは、ある条件下にある囚人が、自分の不利益を承知の上で、必ず自白してしまうというジレンマを示すユースケースです。
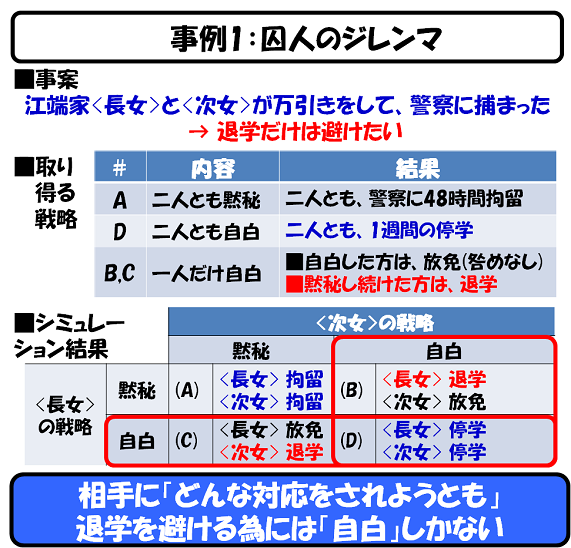
江端家の<長女>と<次女>が、本屋で万引きをして警察に捕まり、彼女たちは別々の取調べ室で聴取を受けている、と仮定しましょう。
彼女たちが2人とも「万引きしていない。レジの場所が分からずに、気がついたら外に出てしまっていたのだ」と主張し続ければ、2人とも警察に2日程度、拘留されるだけで済みます(ケース(A))。
ところが、<長女><次女>の一方が、「ごめんなさい。万引きしました」と先に自白してしまえば、自白した側は、褒められた上に、すぐに釈放してもらえます。しかし、その状況にあって、なお、黙秘を続けた側は、「即時退学」となってしまいます(ケース(B)(C))。
もし2人とも自白してしまえば「停学」になります(ケース(D))。復学後の学園生活は、先生や友人に白い目で見られたり、陰口を言われたりして、楽しくないものになるのは確実ですが、それでも「退学」だけは免れます。
この場合、彼女たちの取る戦略はどうなるか ―― 必ず<長女>も<次女>も自白してしまうのです。
ここで大切なことは、<長女>と<次女>が別々の取り調べ室にいて、お互いに状況を知り得る手段がないという点にあります。どちらかが、「おい、もう、あいつ(<長女>or<次女>)は自白したぞ」と、虚偽の情報を与えられたら、もう、自白する以外に、「退学」を回避する手段がないからです。
このように、<長女>と<次女>の両方が黙秘を続けること(ケース(A))が、その2人にとって最大利益戦略であることが明々白々であるのに、その戦略が取れない状況に陥り(ケース(D))、そこから動けなくなってしまうことを「ナッシュ均衡」といいます。
<長女>も<次女>も、ナッシュ均衡によって、最善の手は打てないまでも、それでも「自白」という戦略によって、「退学」という最悪の選択を避けることには成功するわけです。
これこそが、「最悪の状況下で、最終ラインを確保する」という、ゲーム理論の神髄です。
Copyright © ITmedia, Inc. All Rights Reserved.
Special Contents
- PR -Special Contents
- PR -Special Contents 1
- PR -Special Contents 2
- PR -記事ランキング
- TSMCがGaN事業撤退へ、ロームは「さまざまな可能性を協議」
- 講演会場が静まり返った――中国が生み出した衝撃のトランジスタ構造
- TSMCがGaNファウンドリー事業から撤退へ、NavitasはPSMCと提携で対応
- 26年度には世界大手の9割が採用、黒字化も 本格化するソニーの車載イメージセンサー
- 危うい再建計画 Wolfspeed、CHIPS法補助金で再生図るか
- 25年5月の世界半導体市場は全地域で成長、19.8%増の590億ドルに
- 「DRAM生産の4割を米国で」 Micronを待ち受ける過酷な競争
- 半導体製造ラインの立ち上げ迅速に、日本IBMが京都に開発拠点
- もみ殻と鉱山副産物で「燃料電池用触媒」、白金の代替に
- 22nmプロセス採用でMRAM内蔵、ルネサスがエッジAI特化の新マイコン