量子コンピュータよ、もっと私に“ワクワク”を:踊るバズワード ~Behind the Buzzword(2)量子コンピュータ(2)(5/9 ページ)
シュレーディンガー方程式の江端流解釈
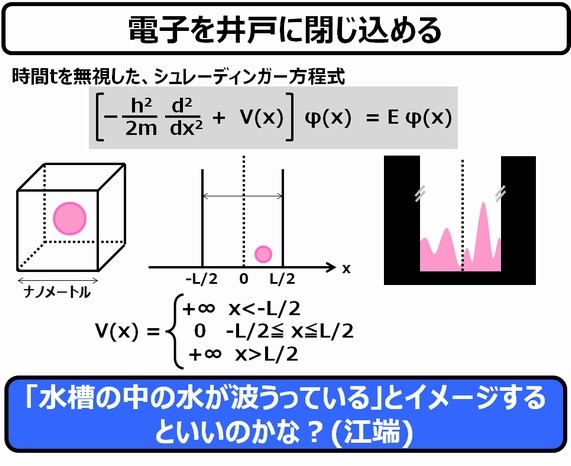
では、その「私なりの理解」を説明させて頂きたいと思いますが、その前に、まずは読者の皆さんが(そして、私も)一番嫌いであろう、数式(シュレーディンガー方程式)から、とっとと片付けていきましょう。
シュレーディンガー方程式とは、物理学の量子力学における基礎方程式です―― といわれると、なんかビビってしまいそうですが、基本的には、(1)運動方程式(ド・ブロイの式)、(2)エネルギー保存法則、(3)波の式、の高校物理の三点セットで導き出せる式 ―― という理解で必要十分です。
上記の式は、位置をx軸上に縛りつけて、かつ時間項tを無視していますが、式の"形"に影響はありません。それと、大学の電子工学科在籍時の癖で、虚数iをjと誤記しているところがありますが、"j"は"i"と読み替えてください(電気の世界では、"i"は電流を意味しますので、混乱がないように"j"を使います)。
シュレーディンガー方程式は、上記の(1)~(3)を混ぜ合わせて、大学の入試問題の定番である、バネの弾性エネルギーと位置エネルギーを使って解く問題を、量子というものすごく小さい世界でも成り立たせるために拡張を行った式、という理解でOKだと思います(実際、シュレーディンガー方程式を、ちょっと弄ると、古典力学のエネルギー保存法則の式の形になります(図中の赤線を参照))。
なぜ、このような面倒くさい式が必要かというと、実は、ここから下に出てくる式が一応根拠のあるものであることを、説明したいからです。後述しますが、ここで大切なことは、量子のエネルギー状態が離散的(バラバラ)に存在するということです。
では、最初に、想定する「電子」をつかった量子ビットのイメージを説明します*)。
*)[Tさんツッコミ!]この方式は「量子ドット方式」と呼ばれる量子コンピュータの方式の一つです。
まず一つの電子を、量子井戸という深い穴にたたき落とします(その「量子井戸」とは何のことか、と問われると、今の私には分かりません。これは次回以降の宿題とさせて下さい)*)。
*)[Tさんツッコミ!]量子ドット方式では、このポテンシャル(深い穴)を、電磁場を用いて実現しているようです。
ここで重要なのは、電子をこの井戸から出られないようにする、ということです。「出られない井戸に入れたのであれば、出られないに決まっているだろう」と考えるのが当然ですが、量子(ここでは電子)は井戸の外と中の両方に同時に存在できるのです ―― トンネル効果です(後述します)。
『井戸の外に、電子の粒の80%が存在するけど、20%は井戸の外に存在しているんですよ』と言われたら、「ああ、確率の話ね」と納得されるかもしれませんが、そういうことではないのです。
正しくは「電子の1つの粒が、井戸の中と外に80%:20%の確率で同時に存在する」ということです ―― なんというか『1つの「粒」である電子が、空間的に雲のように、ボヤっと広がって存在する』というイメージになります。
このお話の「気持ち悪さ」については、前回、散々お話してきました。もう、このフレーズを理解するのは諦めましょう(私は諦めました)。
取りあえず、この量子井戸は、量子のすり抜け(トンネル効果)が発生しないくらい十分に深い(エネルギー障壁が大きい)ものとします。
電子は粒であると同時に波でもあるので、分厚いガラスの水槽の中で揺れている波とイメージすることができるかもしれません(ただし、この考え方を見つけられなかったので、江端の勘違いかもしれません)*)。
*)[Tさんツッコミ!]水槽の水では、両端が自由端反射になってしまいます。量子井戸の場合は固定端反射になる点が異なります(後に出てくる『両端を縛った”縄”』の内容ならOKです)。
で、シュレーディンガー方程式に、この深い井戸に閉じ込められた電子が移動できる範囲(-L/2とL/2)を境界条件とすると、以下の離散(バラバラ)のエネルギーと波の式が出てきます(出てくるんです! ここは私を信じてください!)。
この式も難しいことを書いているように見えますが、実際のところは「団体縄跳びの縄を床の上において、うまく振動させると、縄にいくつもの波を発生させることができる」ことを、数式で表現したものに過ぎません。
縄の片側を縛っておいて、もう片方でゆっくり動かしながら波を作れば、最も単純な波は、縄の中央で最も大きく振れる波が作れますが、素早く動かすことで、複数個の波 Knを作ることができます。素早く動かすのは結構難しくて、疲れる(エネルギーがたくさん必要)ということを示したのがEnです。
ここで重要なのは、縄の両端の位置を固定している限り、波の数は必ず整数値 ―― 離散値になる、ということです。
量子が波の性質を持つ――なるほど、それは分かった(ことにする)。
その波は整数の正弦波の重ね合わせである――うむ、それも分かった(ことにしよう)。
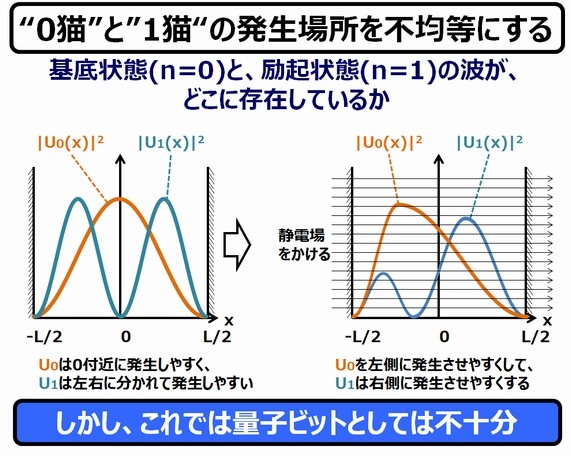
しかし、だからといって「それが何だっていうの?」と問われれば、電子のn=0の波を、"0猫"として、n=1の波を"1猫"とする量子ビットの作り方を説明しているのです。
しかし、電子を普通に放置すれば、n=0の波だけになってしまうだろうし、何か手を加えれば(熱や光を与えれば)、n=1,2,3の波が現われて、"1猫"以外にも、"2猫"、"3猫"、"4猫"、…が登場する「猫カフェ」状態になってしまいます。
そこで、これを2匹の猫だけにすることを考えなければなりません。そのためには"0猫"の食事の量をコントロールしなければなりません。
基本的に、電子は基底状態(n=0)の波の状態にあります。これに所定の光子を加えることで、励起状態(n=1,2,3,…)にすることができます。ということは、逆に言えば、n=0の波は、光子を適切な量加えることによって、n=0の波("0猫")と、n=1の波("1猫")だけを併存させることができるのです。
こうして、"0猫"と"1猫"だけが存在する猫カフェが実現されます(ただしn=2以上の猫を作らないように光子をコントロールすることは必要です)。
ですが、その状態でも、"0猫"も、"1猫"も、井戸の底でドタバタと動き回っていますので、これを判別することができません。これを何とかして"0猫"は井戸の底の左半分(-L/2 から0 の間)、"1猫"は井戸の底の右半分(0からL/2の間)にだけ存在させるようにしたいです。
そこで、次の手段となります。井戸の中に静電場を発生させます。
このように静電場を発生させることによって、"0猫"と"1猫"が滞在する場所(存在確率)は、歪な形となります。"0猫"は、井戸の左側に、"1猫"は井戸の右側に現われやすくなります。
しかし、これでもまだ不十分です。これでは"0猫"と"1猫"を分離して管理・制御できているとは言えず、前述のブロッホ球で表現できる量子ビットにはならないのです。
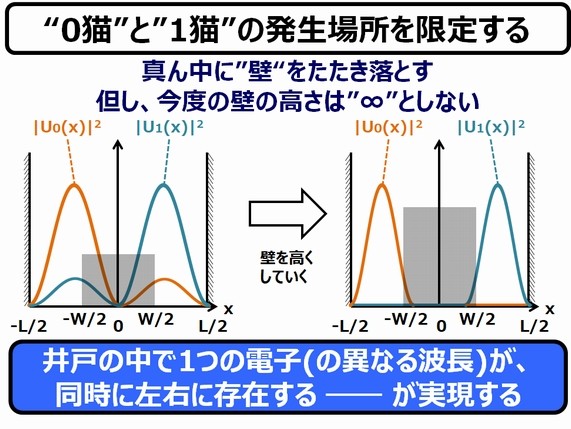
井戸の真ん中に壁をたたき落とす
ここで最後の手段を行います。井戸のど真ん中に壁をたたき落とすのです。
「は? 壁を作るなら、最初から井戸の中に作っておけばよかったんじゃないのか?」と思われるかもしれません。しかし、この壁の高さが"0猫"も"1猫"が通り抜け抜けられるギリギリの高さ(イメージ的には"厚さ"?)に設定する、という点がミソなのです。
もしこの壁のエネルギーが量子のエネルギーより大き過ぎると、そもそも量子が壁に閉じ込められて、"0猫"も"1猫"も、右か左のいずれか一方にしか存在できません。しかし、壁が低過ぎると(壁のエネルギーよりも電子のエネルギーが大きければ)、軽々と壁を通り抜けえてしまって、ネコは井戸の底のどこにでも移動できてしまいます。
1つの電子を、左右のどちらにも存在させるには、この、一定の確率で壁のエネルギーよりも小さいエネルギーの量子が、壁を擦り抜けてしまうという ―― これまた量子の特有で、ものすごく気持ちの悪い性質 ―― 「トンネル効果」を使うことになります。
このトンネル効果によって、"0猫"は、ほとんどの場合井戸の左側にいるけど、ごくまれに右側にいることもあり、一方、"1猫"は、ほとんどの場合井戸の右側にいるけど、ごくまれに左側にいることもある、という状況が出来上がります。
以上、非常に面倒くさいプロセスではありましたが、このようにして、"0猫"と"1猫"を区別しつつ併存させることが可能な、量子ビットが実現されることになります。
ただ、私は、(1)この井戸の実現方法や、(2)井戸の中にたたき落す壁の作り方、(3)電子1個を井戸の中に放り込む方法、そして、(4)静電場の与え方など、具体的な実現手段は何一つ分かっていません。加えて、これらの量子を使った量子ゲートの作り方についてはイメージすらできていません。
まあ、とりあえず、古典ビットとは比較にならないほど面倒くさいプロセスを経て、量子ビット1つを作れそうだ、ということは分かりましたので、今回はここまでにしておきたいと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
Special Contents
- PR -Special Contents 1
- PR -Special Contents 2
- PR -記事ランキング
- 2024年の半導体市場は21%成長 NVIDIAが初の首位に
- 半導体メーカーの「悲喜こもごも」 絶好調のTSMC、人員削減のST
- IntelがAltera売却へ、株式51%を米投資ファンドに
- 1インチサイズの全固体電池を10秒で作製 レーザーで加工
- ミネベアミツミが芝浦電子買収へ 「8本槍」戦略強化に向け
- 2035年のウエハー需要を予測する ~半導体も「VUCA時代」に
- ソフトバンクが買収したAmpereの「流転の生涯」をたどる
- トランプ政権の「アメとムチ」 Intelは補助金を受け取れるのか
- AIのデータ転送問題解決に王手、シリコンフォトニクス新興企業
- パワー半導体市場、25年後半に在庫が正常化 26年から成長拡大